$\setCounter{0}$
Part 1: The wave vector
Part 2: The interface
Part 3: The s-polarization
Part 4: The p-polarization
Part 5: Multilayers
In a five-piece series of posts I will define and derive the Fresnel’s coefficients for reflection and transmission of plane waves on the interface between vacuum and isotropic material. It is going to be somewhat standard textbook explanation, but with three twists:
- we will use the HL units as defined in the previous blog
- we will keep isotropic permeability \(\mu\) – in this way we sneak in the possibility of negative index of refraction
- we will introduce the geometrical components of the wave vectors
So, let’s start from the Maxwell’s equations for HLU fields in the absence of external charges or currents
\(\DeclareMathOperator{\Div}{div}
\DeclareMathOperator{\Rot}{rot}
\newcommand{\parder}[2]{\frac{\partial {#1}}{\partial {#2}}}
\begin{align}
\begin{aligned}
\Div\mathbf{D} &=0,
&\Rot\mathbf{H} &=\frac{1}{c}\parder{\mathbf{D}}{t},
\\
\Rot\mathbf{E} &=-\frac{1}{c}\parder{\mathbf{B}}{t},
&\Div\mathbf{B} &=0.
\end{aligned}
\end{align}\)
The induced polarization and currents are captured in the material relations, here we will keep the \(\varepsilon\) and \(\mu\) as scalars:
\(\begin{align}
\begin{aligned}
\mathbf{D} &=\varepsilon\mathbf{E},
\\
\mathbf{B} &=\mu\mathbf{H}.
\end{aligned}
\end{align}\)
We consider the \(\bf{E}\) and \(\bf{H}\) to be the base fields, the \(\bf{D}\) and \(\bf{B}\) as linear response of the material, and we look for some solution in the form of plane wave:
\(\begin{align}
\begin{aligned}
&\mathbf{E}(\mathbf{r},t) = \mathbf{E}_{\mathbf{k},\omega} e^{i(\mathbf{kr}-\omega t)},
\\
&\mathbf{H}(\mathbf{r},t) = \mathbf{H}_{\mathbf{k},\omega} e^{i(\mathbf{kr}-\omega t)},
\end{aligned}\label{eqAmplitudes}
\end{align}\)
where \(\mathbf{E}_{\mathbf{k},\omega}\) \(\mathbf{H}_{\mathbf{k},\omega}\) are amplitude vectors for one chosen linear polarization. We will deal with this one particular component and rely on the linearity of Maxwell’s equations that the whole field can be written as some integral over the \(\bf{k}\) and \(\omega\) components and the two polarizations. We will also assume that the \(\varepsilon\) or \(\mu\) may depend on frequency \(\omega\), but not on \(\bf{k}\).
So let’s work on the Maxwell’s equations one by one:
\(\Div\mathbf{D} = \varepsilon\Div\mathbf{E} = \varepsilon\nabla\cdot\mathbf{E} = i\varepsilon\mathbf{k}\cdot\mathbf{E} = 0,\)
so unless the \(\varepsilon\) is zero – case which we will disregard for the moment – we get
\(\begin{align}\label{eqkE}
\mathbf{k}\cdot\mathbf{E} = 0.
\end{align}\)
Meaning that the electric field vector \(\mathbf{E}\), as well as the amplitude \(\mathbf{E}_{\mathbf{k},\omega}\), is always perpendicular to the direction of propagation.
Next:
\(\begin{align*}
\Rot\mathbf{H} = \nabla\times\mathbf{H} = i\mathbf{k}\times\mathbf{H}\; =\; \frac{1}{c}\parder{\mathbf{D}}{t} = \frac{\varepsilon}{c}\parder{\mathbf{E}}{t} = -i\varepsilon\frac{\omega}{c}\mathbf{E},
\end{align*}\)
which we will write for the moment as:
\(\begin{align}
\frac{\omega}{c}\mathbf{E} = -\dfrac{\mathbf{k}\times\mathbf{H}}{\varepsilon},
\end{align}\)
meaning that the \(\bf{E}\) and \(\bf{H}\) fields are proportional and orthogonal.
Third one:
\(\begin{align*}
\Rot\mathbf{E} = \nabla\times\mathbf{E} = i\mathbf{k}\times\mathbf{E}\; =\; -\frac{1}{c}\parder{\mathbf{B}}{t} = -\frac{\mu}{c}\parder{\mathbf{H}}{t} = i\mu\frac{\omega}{c}\mathbf{H},
\end{align*}\)
which we will again write as:
\(\begin{align}
\frac{\omega}{c}\mathbf{H} = \dfrac{\mathbf{k}\times\mathbf{E}}{\mu}.
\end{align}\)
And for \(\mu\) not equal to zero, analogically to \eqref{eqkE}, the last one simply yields:
\(\begin{align}
\mathbf{k}\cdot\mathbf{H} = 0.
\end{align}\)
Further, we define \(\boldsymbol\kappa\) as the geometrical component of the wave vector
\(\begin{align}
\mathbf{k} = \frac{\omega}{c}\boldsymbol\kappa,
\end{align}\)
and using \(\boldsymbol\kappa\), we cancel the \(\omega / c\) from all four equations
|
\(\begin{align} \begin{aligned} \boldsymbol\kappa\cdot\mathbf{E} &= 0, &\mathbf{E} &= -\dfrac{\boldsymbol\kappa\times\mathbf{H}}{\varepsilon}, \\ \mathbf{H} &= \dfrac{\boldsymbol\kappa\times\mathbf{E}}{\mu}, &\boldsymbol\kappa\cdot\mathbf{H} &= 0. \end{aligned} \label{eqRedMax} \end{align}\) |
This set of equations can be understood for both sides of eqs. \eqref{eqAmplitudes}, i.e. either for the \(\bf{E}\) and \(\bf{H}\) transients, or, after cancelling the factor \( e^{i(\mathbf{kr}-\omega t)} \), for the amplitudes \(\mathbf{E}_{\mathbf{k},\omega}\) and \(\mathbf{H}_{\mathbf{k},\omega}\). Later we will think in terms of the amplitudes, but we will drop the subscript \(\mathbf{k},\omega\).
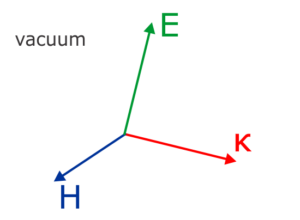
For the simplest case of vacuum with \(\varepsilon = 1\) and \(\mu = 1 \) we can see that \(\boldsymbol\kappa , \bf{E} , \bf{H}\) form an orthogonal right-handed system.
Next, we insert the third equation of \eqref{eqRedMax} into second and move the constants on the left-hand side, obtaining:
\(\begin{align*}
-\varepsilon\mu\mathbf{E} = \boldsymbol\kappa\times ( \boldsymbol\kappa\times\mathbf{E} ).
\end{align*}\)
To the right-hand side we apply the “bac-cab” identity (see footnote):
\(\begin{align*}
-\varepsilon\mu\mathbf{E} = \boldsymbol\kappa\cdot ( \boldsymbol\kappa\cdot\mathbf{E} ) – \mathbf{E}\cdot ( \boldsymbol\kappa\cdot\boldsymbol\kappa ).
\end{align*}\)
Finally, we use the first eq. from \eqref{eqRedMax} to remove the first term on the right hand side. The equation must hold for any \(\bf{E}\), therefore
| \(\begin{align} \varepsilon\mu = \boldsymbol\kappa\cdot\boldsymbol\kappa. \end{align}\) |
This is the dispersion relation, only the physical dispersion has been removed from it. And that’s what we want, to see the geometry clearly.
Examples
In the vacuum case, \(\varepsilon = 1\) and \(\mu = 1 \), we can choose the direction of propagation along z-axis, \(\boldsymbol\kappa = (0,0,\kappa_{z}) \) and fix the electric field amplitude along x-axis, \( \mathbf{E} = (E_0,0,0) \). We get \( \kappa_z = 1 \) and the magnetic field amplitude is then \( \mathbf{H} = (0,E_0,0) \). The HLU field amplitudes in vacuum are the same.
If we replace the vacuum with simple transparent dielectric with \( \varepsilon > 1 \) and \(\mu = 1 \), we have \( \varepsilon = \kappa_z^{2} \), so \( \kappa_z = \sqrt{\varepsilon} \equiv n \), which means that the size of the geometrical wave vector is the (positive real) refractive index. The magnetic field amplitude is then \( \mathbf{H} = (0,n E_0,0) \), so the magnetic field is now greater than in vacuum, but it should be understood that for the same magnetic amplitude, the electric amplitude is smaller, as some of the electric field strength is spent polarizing the dielectric. For the same frequency, the wave vector is longer than in vacuum, so for the same period, the wavelength is shorter, means the phase of the wave propagates slower.
Other interesting case is the pure metallic response with \( \varepsilon < 0 \), where \( \kappa_z = \sqrt{\varepsilon} \equiv ik \), and \(k\) being the positive real absorption coefficient. Here we have non-propagating, pure evanescent wave in the positive z-direction. The magnetic field amplitude is \( \mathbf{H} = (0,i k E_0,0) \), so the magnetic field oscillation is \( \pi/2 \) shifted with respect to the electric field.
Eventually, for general dielectric response, \(\varepsilon = \varepsilon_1 + i\varepsilon_2 \), we can have any value of \( \varepsilon_1 \) while \( \varepsilon_2 \) is non-negative, so we have \( \kappa_z = \sqrt{\varepsilon} \equiv N = n+ik \). For wave propagating and diminishing along positive direction of z-axis both real and imaginary part of \( \kappa_z \) must be non-negative.
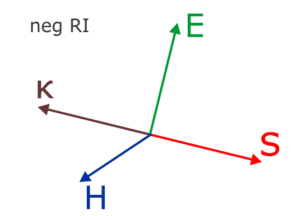
Then we have the curious case when we start to mix in the permeability \( \mu \), because we can reach a situation, when both the real parts of \( \varepsilon \) and \( \mu \) are negative (while the imaginary parts are non-negative). So looking at \( \varepsilon\mu = \kappa_z^{2} =(n+ik)^{2} \), the only way to get non-negative \( k \) is to have negative \( n \). Or, for purely real negative \( \varepsilon \) and \( \mu \), one can look at the fields from \eqref{eqRedMax} to realize that to achieve Poyinting vector, \( \mathbf{S} = c\mathbf{E}\times\mathbf{H}^\ast \) (energy flow, in HLU), oriented in positive z-direction, the \( \kappa_z \) must be negative.
We introduced the nabla operator:
\(
\newcommand{\parder}[2]{\frac{\partial {#1}}{\partial {#2}}}
\nabla \equiv (\parder{}{x},\parder{}{y},\parder{}{z}).\)
Used identity
\(
\mathbf{a} \times ( \mathbf{b} \times \mathbf{c} ) =
\mathbf{b} \cdot ( \mathbf{a} \cdot \mathbf{c} ) –
\mathbf{c} \cdot ( \mathbf{a} \cdot \mathbf{b} ).
\)