In ellipsometry we deal with polarization, angles, rotations and reflections, so it becomes crucial to define properly the coordinate system. With that comes also the need for conventions declaring what will be understood as positive/negative direction and sense of rotation. Particularly the fact that we experience the mirror reflection brings possible ambiguity and presents source of sign confusion.
What I want to discuss in this post is one principal choice between two possible conventions known as Fresnel’s and Verdet’s convention. They determine the choice of direction in which the p-polarized component of reflected light is measured.
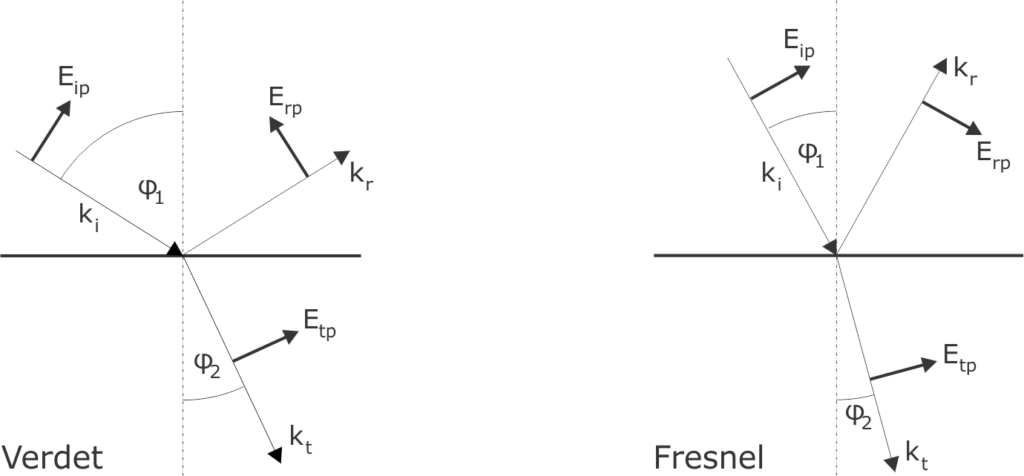
The figure above illustrates the idea. We have a planar interface and incoming wave \(\mathbf{k_{i}}\), which is partly reflected, \(\mathbf{k_{r}}\), and partly transmitted, \(\mathbf{k_{t}}\), into the medium. The plane of the figure is the plane of incidence. In this configuration, the polarization of any of the beams is described in components that are perpendicular (s-polarization) and parallel (p-polarization) to the plane of incidence. There is no dispute over the direction of the s-polarization, which points out of plane towards the reader for each of the incident, reflected and transmitted beams. The difference is – as depicted on the drawing – in the orientation of the \(\mathbf{E_{rp}}\) component, or in other words, in which direction the reflected p-polarized \(\mathbf{E}\) field is considered as positive. In the following I will try to explain the underlying philosophy for the Verdet or Fresnel approach.
The Verdet picture is the one you will find in most textbooks, especially in those related to ellipsometry. When we want to track the changes of the polarization state of the light as it passes through the optical system of the ellipsometer, it is convenient to use a right handed basis \(\mathbf{k,p,s}\), which travels along with the beam and to describe the polarization state using Jones vector in the \(\mathbf{p,s}\) basis. Then each of the components along the beam (polarizer-compensator-sample-analyzer for instance) is represented by Jones matrix and the sample becomes just another device changing the polarization – only with unknown Jones matrix components, which we want to determine. The whole setup can be depicted as a sort of transmission experiment.

This means that if we actually set the ellipsometer to straight-through (see-through, \(\phi=90^\circ\)) mode without any sample and perform a measurement, the empty sample space is represented trivially by unitary Jones matrix and the result in terms of ellipsometric angles should be \(\Psi=45^\circ\) and \(\Delta=0^\circ\).
The limit of normal incidence (\(\varphi=0^\circ\)) becomes awkward, since there should be no distinction between s- and p-polarization (on isotropic sample), but we are forced to define the Fresnel’s reflection coefficients as opposite, \(r_{\perp} = r_s = -r_p\).
On the other hand, the Fresnel convention becomes more useful when we want to have a closer look on the sample and see what the fields are doing. Any theory that describes the wave propagation and mixing in multi-layered sample will be formulated in terms of propagation along the axis perpendicular to the surface, using the field components in the plane of the interfaces. The resulting formalism can be understood as generalization of the normal incidence and the Fresnel’s convention gives the consistent expression for the normal incidence reflection coefficients, i.e. \(r_{\perp} = r_p = r_s\) (on isotropic system).
While the normal incidence is a borderline limit case of the ellipsometric experiment, in the straight-through configuration, the empty sample space still inverts the p-direction, so the experiment yields \(\Psi=45^\circ\) and \(\Delta=\pm 180^\circ\). This might be seen as a bug until we realize that it is simply different experiment – no reflection occurred.
In the scope of this blog – as in the rest of my work – I will stick to the Fresnel’s picture. Moreover, I tend to express the Fresnel’s coefficients directly as ratios of the x and y components of the electric fields, \(E_{x}, E_{y}\). This is illustrated on the figure below. Since the angle of incidence is equal to the angle of reflection, then \(r_x = E_{rx} / E_{ix}\) is equivalent to \(r_p = E_{rp} / E_{ip}\) (in Fresnel’s convention), but the \(t_x = E_{tx} / E_{ix}\) is not equal to \(t_p = E_{tp} / E_{ip}\) as usually found in the books.
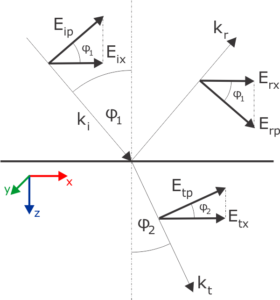
We will see in one of the next blog posts that such approach leads to more symmetric formulas and typically does not bring any confusion: In typical ellipsometry experiment we ignore the transmitted beam. In the rare cases when we actually do want to measure the polarization state of the beam transmitted through planar sample, we do it again in the far field in the ambient medium. That means that the refraction angle of the transmitted beam is equal to the incidence angle and so the \(t_x\) is equal to \(t_p\). In the remaining situations which do not fulfill these conditions, we just need to keep this distinction in mind.
The issue of sign conventions and related confusion has been thoroughly discussed by R.T.Holm1 and I recommend reading the text as it covers many topics that we will discuss on this blog. In the course of several following blog post I will go through various parts of the discussion, but instead of presenting different possible choices I will present consistent analysis of one particular choice and discuss the consequences. Of course, I don’t want to claim that my choice is the right one, but I will go some way in advocating why do I prefer such choice. In some later stage I will want to explore areas that are not covered in standard textbooks and are very susceptible to sign confusion. These areas include the time-domain terahertz ellipsometry with its intrinsic ability to determine the phase of the detected waves; materials with magnetic \(\mu\) response with the possibility of negative refractive index; and materials with magneto-electric coupling in constitutive relations.
As soon as we arrive to anisotropic samples, we will need to have more careful look on the coordinate system conventions, so this topic will be revisited few times over the course of this blog.
1 R. T. Holm, “Convention confusions”, in Handbook of Optical Constants of Solids II, edited by E. D. Palik, chapter 2, 21-55, Academic Press, San Diego (1991).